The concept of the modulus of elasticity was first introduced by the British physicist and physician Thomas Young in 1807. For this reason, the term is often referred to in the literature as Young’s Modulus. By developing this concept, Young provided a quantitative means of describing how materials deform under mechanical forces.

Definition

The modulus of elasticity (E) is a measure of a material's tendency to deform when a force is applied. It quantifies the ratio of stress (force per unit area) to strain (relative deformation) within the elastic region of a material's behavior. In simple terms, it expresses how stiff or flexible a material is:

• A high modulus indicates that the material is rigid and resists deformation.
• A low modulus means the material is flexible and deforms more easily.

$E = \frac{σ}{𝜀}$

Where:

• E = Modulus of elasticity (Pa)
• $σ = Stress =\frac{F}{A}$
• $ε = Strain = \frac{ΔL}{L 0}$

Derivation and Basic Unit

This value is derived from the stress-strain curve obtained during a tensile or compression test. In the linear elastic region of this curve, the slope of the line corresponds to the modulus of elasticity.

This linear behavior is described by Hooke’s Law, given by the equation:

σ=E⋅ε

Hooke’s Law applies only within the elastic (linear) region. Once the material reaches the plastic deformation region, this linearity breaks down, and Hooke’s Law is no longer valid. In such cases, the modulus may vary with the applied load.

The SI unit of the modulus of elasticity is the Pascal (Pa), defined as:

$1 Pa = 1\frac{N}{m^2}$

In practice, larger units such as MPa (10⁶ Pa) or GPa (10⁹ Pa) are commonly used.

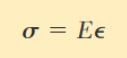
^{Hooke's Law}

Example Materials

E_Steel = 2x10¹¹ N/m²

E_Aluminum = 7x10¹⁰ N/m²