Euler's number, a significant constant in mathematical calculations and scientific modeling, is an irrational number approximately equal to e = 2.718281. Like Pi (π), Euler's number does not have a finite decimal representation but instead represents a value that continues without interruption on the number line. This number is especially used as the base of natural logarithms and, although named after Leonhard Euler, was discovered by the Swiss mathematician Jacob Bernoulli.
The mathematical definition of Euler's number is made through a limit expression and is most fundamentally expressed as:
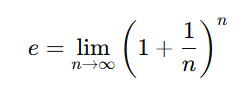
This expression arises particularly in modeling situations such as compound interest calculations and exponential growth. Another significant feature of Euler's number is its direct connection to exponential functions. Among these functions, the one defined as y=ex represents exponential growth or decay.
The value of Euler's number can be increasingly accurately determined by calculating consecutive terms. For example, as the value of n increases, the following limit expression approaches the value of Euler’s number:

Thus, Euler's number is used not only in mathematical calculations but also to model a variety of phenomena in physics, economics, and biology.
Applications of Euler's Number
Euler's number has a broad range of applications across various fields:
1. Exponential Growth and Decay: Natural processes such as population growth, bacterial growth, and radioactive decay are often described by exponential growth or decay, which can be modeled using Euler's number.
2. Continuous Compound Interest: In economic calculations, particularly in continuous compound interest computations, Euler’s number plays a key role.
3. Natural Processes: Euler’s number is also used to describe natural events such as heat transfer and disease spread. These phenomena can be modeled using exponential growth and decay laws.
4. Probability Theory: Euler’s number appears in probability theory as well. For example, the probability of a gambler losing all bets after n plays on a slot machine approaches 1/e.
Mathematical Definitions of Euler’s Number
Euler's number can be defined through limits and infinite series. In the limit definition:
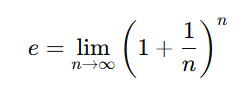
This expression represents a value that approaches Euler’s number as n tends to infinity. Euler's number can also be defined as the result of an infinite series:
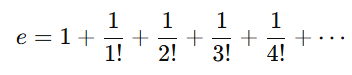
By taking the first few terms, we can approximate e as follows:
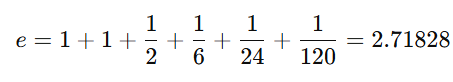
Euler’s number, as the base of natural logarithms, is a fundamental constant in mathematical and scientific modeling. It has a wide range of applications from biology to economics, from physical processes to probability theory. As an important tool in both theoretical and practical calculations, Euler's number plays a critical role, particularly in exponential growth, decay, and continuous compound interest calculations.


