Maxwell's equations are the four fundamental equations that describe the relationship between electricity and magnetism. Developed by James Clerk Maxwell in the 19th century, these equations laid the groundwork for modern theories of electric and magnetic fields. They play a crucial role not only in theoretical physics but also in engineering and technological applications, explaining how electric and magnetic fields interact.

In the 19th century, scientists sought to understand the interactions between electric and magnetic fields. Discoveries by figures such as Michael Faraday and André-Marie Ampère were unified by James Clerk Maxwell, who formulated them into four equations. Maxwell's work revealed that electric and magnetic fields dynamically interact, and these interactions are governed by fundamental laws, which are encapsulated in these four equations.

^{James Clerk Maxwell}

Maxwell's Equations

Maxwell's equations consist of four primary equations:

1. Gauss's Law (for Electric Fields)
2. Gauss's Law (for Magnetic Fields)
3. Faraday's Law of Induction
4. Ampère-Maxwell Law

These equations describe how electric charges and currents influence electric and magnetic fields.

Gauss's Law (for Electric Fields)

Gauss's law describes how electric fields are distributed around electric charges. The total electric flux through a closed surface is proportional to the enclosed electric charge. Mathematically, it is expressed as:

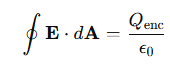Here, Q_enc​ represents the total electric charge enclosed within the surface [C], and ϵ₀ is the electric constant [F/m]. This equation shows the relationship between electric fields and charges.

Gauss's Law (for Magnetic Fields)

Gauss's law for magnetism states that magnetic field lines are always closed loops and that there are no magnetic monopoles. The total magnetic flux through a closed surface is zero:

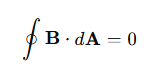This equation indicates that there are no isolated magnetic charges; instead, magnetic field lines always form closed loops.

Faraday's Law of Induction

Faraday's law explains how a time-varying magnetic field induces an electric current. This phenomenon is the basis for electromagnetic induction, and the law is expressed as:

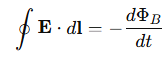In this equation, Φ_B​ represents the magnetic flux [Wb], and the negative sign indicates that the induced current opposes the change in the magnetic field.

Ampère-Maxwell Law

Ampère's law states that electric currents produce magnetic fields. However, Maxwell extended this law by including the effect of time-varying electric fields, which also produce magnetic fields. The law is expressed as:

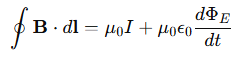Here, μ₀ is the magnetic permeability [H/m], and I is the electric current. The second term represents the contribution of the time-varying electric field to the magnetic field.

Applications of Maxwell's Equations

Maxwell's equations have numerous important applications in both theoretical and practical realms. They play a fundamental role in understanding the propagation of electromagnetic waves, such as radio waves, light, and other types of electromagnetic radiation. Technologies such as electrical circuits, motors, generators, and wireless communication can all be explained using these equations.

Maxwell's equations represent a scientific breakthrough that unifies electric and magnetic fields. These equations have laid the foundation for electromagnetic theory and have driven many advancements in modern physics and engineering. Maxwell's work not only unified electric and magnetic fields but also paved the way for understanding light as an electromagnetic wave. As a result, Maxwell's equations are a cornerstone of both scientific and technological progress.